Számvizsgáló (minta)
Kategória: korábbi évek excel - emelt szint
Feladat leírása

A pozitív egész számoknak sok érdekes jellemzője van, de ki tudja hirtelen, melyik szám
mitől is különleges? Készítsen az 1 és 25000 közötti pozitív egész számok néhány
tulajdonságát vizsgáló táblázatot! A számok néhány adatát és a számítások elvégzésére
előkészített néhány további munkalapot tartalmazó szamvizsgalo-forras állományt
megtalálja a Források mappában.
A megoldás során vegye figyelembe a következőket:
- Segédszámításokat a segéd nevű munkalapon végezhet munkája közben!
- Amennyiben lehetséges, a megoldás során képletet, függvényt, hivatkozást használjon,
hogy az adatok módosítása esetén is a kívánt eredményt kapja! - Ha egy részfeladatban fel akarja használni egy korábbi részfeladat eredményét, de azt
nem sikerült teljesen megadnia, használja a megoldását úgy, ahogy van, vagy írjon be
egy valószínűnek tűnő eredményt, és azzal dolgozzon tovább! Így ugyanis pontokat
kaphat erre a részfeladatra is. - Ha egy részfeladatban fel akarja használni egy korábbi részfeladat eredményét, de azt
nem sikerült teljesen megadnia, használja a megoldását úgy, ahogy van, vagy írjon be
egy valószínűnek tűnő eredményt, és azzal dolgozzon tovább! Így ugyanis pontokat
kaphat erre a részfeladatra is.
Részfeladatok
1. Nyissa meg a szamvizsgalo-forras állományt majd mentse el szamvizsgalo néven a program alapértelmezett formátumában!
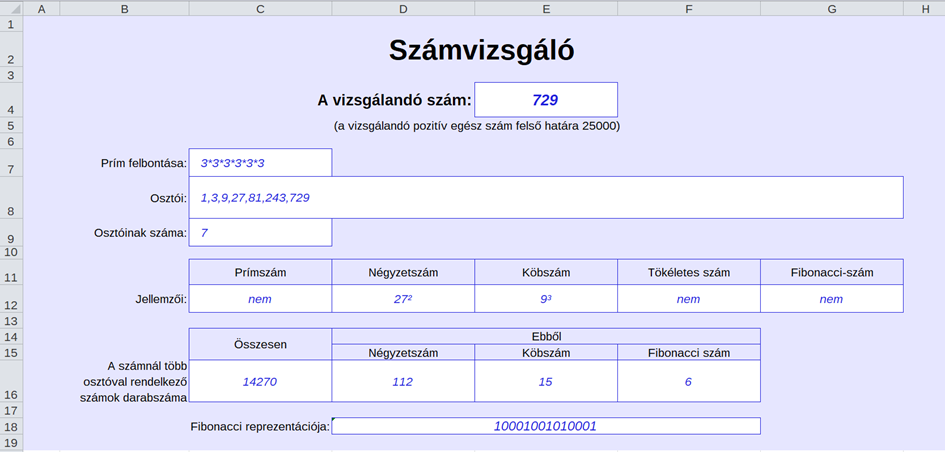
2. Írjon be egy tetszőleges pozitív egész számot a vizsgáló munkalap E4-es cellájába, majd a „Hibás!” szöveget az F4-es cellába a kitöltéssel megegyező betűszínnel, hogy alaphelyzetben ne látsszon. Feltételes formázással érje el, hogy 25 000-nél nagyobb szám beírása esetén a „Hibás!” felirat piros színnel és szegélyezve megjelenjen!
3. A C7, C8 és C9 cellákba jelenítse meg a vizsgálandó szám prímtényezős felbontását, osztóit és osztóinak számát (ezeket tartalmazza a számok munkalapon található adattábla)!
a) A táblázat C12, F12, G12 celláiba másolható képlet segítségével jelenítsen meg „igen” vagy „nem” értéket attól függően, hogy a vizsgált szám prímszám, tökéletes szám, illetve Fibonacci-szám-e.
b) Az D12 cellába képlet segítségével jelenítse meg
a) annak a számnak a négyzetét, amely szám négyzete a vizsgált szám, ha a vizsgált szám négyzetszám (pl. 729 esetén a megjelenített érték: 27²);
b) a „nem” értéket, ha a vizsgált szám nem négyzetszám
c) Az E12 cellába képlet segítségével jelenítse meg
a) annak a számnak a köbét, amely szám harmadik hatványa a vizsgált szám, ha a vizsgált szám köbszám (pl. 729 esetén a megjelenített érték: 9³);
b) a „nem” értéket, ha a vizsgált szám nem négyzetszám.
4. A C16:F16 tartomány celláiba adatbázisfüggvények segítségével határozza meg a vizsgált számnál több osztóval rendelkező, az egyes kategóriákba tartozó számok darabszámát. A képletekhez szűrési táblázatot a segéd munkalapra készíthet. Az adatbázis tartományra ab néven is hivatkozhat.
5. A Zeckendorf-tétel szerint minden pozitív egész szám felírható különböző Fibonacci számok összegeként, s ha a Fibonacci-számok között nem lehet két egymást követő, akkor ez a felírás egyértelmű is. E tételre alapulva beszélhetünk Fibonacci-számrendszerről, melyben csak 1 és 0 számjegyek szerepelhetnek, a helyi értékek pedig az egymást követő Fibonacci-számok. A következő feladatrészben a vizsgált szám Fibonacci-számrendszerbeli alakját határozzuk meg.
6. Az átváltást a fibonacci munkalapon végezze. Ehhez először vegyen fel két 1-es értéket az A21 és A22 cellákba, majd a A2:A20 cellák mindegyikében számítsa ki az alatta lévő két cella tartalmának összegét, ily módon legenerálva az első húsz Fibonacci számot.
7. A B oszlopban képezzük a Fibonacciszámrendszerbe átváltott alak számjegyeit. A B2 cellába kerüljön 1, ha a vizsgál munkalapon megadott szám nem kisebb az A2 cellában lévő Fibonacci-számnál, egyéb esetben ne jelenjen meg semmi.
8. A B3:B21 tartomány celláiba akkor kerüljön 1-es, ha a vizsgált szám nem kisebb az eddig 1-essel jelölt és az aktuális cella melletti Fibonacci számok összegénél. Ha ez nem teljesül, de a cella feletti tartományban volt már 1-es számjegy, akkor a cella értéke legyen 0, egyéb esetben ne jelenjen meg semmi. Tegye másolhatóvá a képletet!
9. A vizsgáló munkalap D18 cellájában jelenítse meg a számjegyek összefűzött sorát!
10. A fibonacci munkalap C2:C21 celláiban jelenítse meg a szám Fibonacciszámrendszerbeli számjegyeinek valódi értékét! Ha az adott sorban a B oszlopban 1-es érték szerepel, akkor jelenítse meg az A oszlopban lévő Fibonacci számot, egyéb esetben legyen 0 a cella értéke.
11. Készítsen oszlopdiagramot a vizsgáló munkalapon az eddig elkészült táblázat alá, azzal megegyező szélességben a számjegyek valódi értékeinek szemléltetésére! A diagram címe „Fibonacci-alak – számjegyek valódi értéke” legyen, a diagram ne tartalmazzon se jelmagyarázatot, se tengelyfeliratot a kategória tengelyen.